Reading the Bones - Tension Dice
I've recently discovered the Angry GM's Tension Pool mechanic, which is quite ingenious. You should go read that now if you've not seen it before. I'll wait.
…
To sum up: keep a ceramic, glass or metal cup or container handy in the center of the playing table where everyone can see it. Periodically toss a d6 into the cup, and watch as the noise magically ratchets up the tension. It's a great tool for sessions that are heavy on exploration and social encounters, to give the players a sense of the passing of time, and keep them guessing a bit about what sort of complication the dice will generate next. I like making one of the players volunteer to roll my cup which is ceramic, dark with moody glazing, and sounds fantastic.
But, what are the odds of rolling at least one '1', indicating an encounter or complication has occurred?
Never Tell Me The Odds #
Alright, I'll show you then:
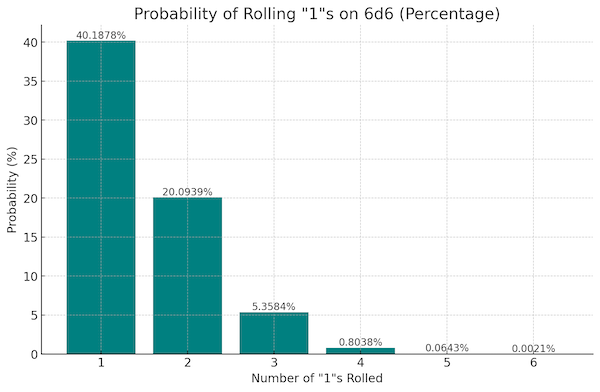
So, given fair dice and a full tension dice pool (cup), there's a 40% chance that something occurs. Intuitively, that seems reasonable, given the length of a typical session, let's say you collect and roll 4 tension pools to check for random complications/encounters. The odds of having at least one encounter in all that is pretty high, 87%. That's good, because while not certain to occur it is likely something has arisen. I mean, if nothing ever happened, what was the point of this whole exercise?
On Rarity/Impact #
Ok. Something has occurred. How impactful should it be on the current events and in-game goals? We'd like to randomly choose this, but intuitively, it should be less likely that high impact events occur than mundane or minor encounters. The procedure outlined in the Angry DM post calls for rolling 1d8 and 1d12 together, and checking the result of a table with values 2-20. This is an interesting choice, and I confess I haven't yet seen the light when it comes to the probability distribution this produces:
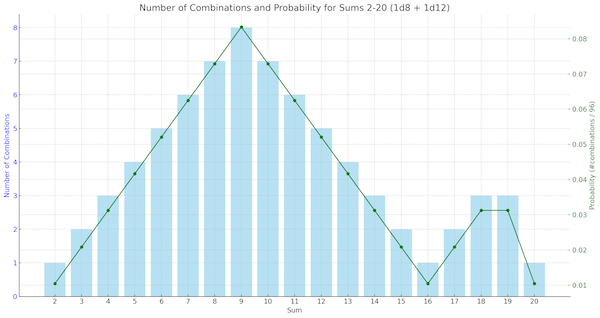
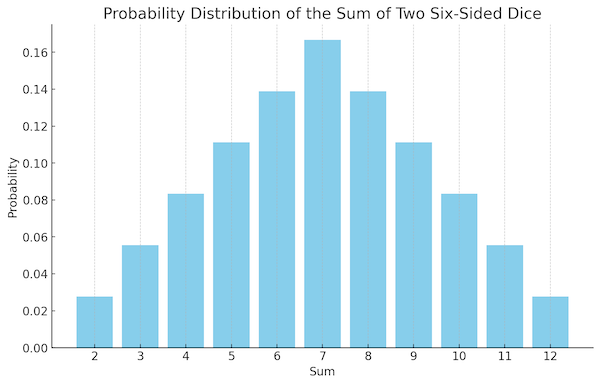
There's a lot more ways to roll a '9' than a '2', '16', or '20' with this system. I find that a bit hard to reason about, versus a distribution produced by two dice of the same size, say 2d6:
SJGames' Skull Dice #
I picked up a set of skull dice at a local store that I thought would work well as Tension Dice. A bit like this, though I got red instead of orange:

I noticed that there were four pairs of two colored dice. Immediately, I realized you could group these into 3 separate 2d6 distributions when you rolled the dice pool, and I wanted to take maximum advantage of that.
Don't Throw Those Bones Away, Read 'Em #
With just a single roll of the Tension Dice you can divine:
- If an encounter occurs
- How impactful it is
- What creature(s) are involved
- What they're doing
- What environmental effects are occurring
- The encounter starting distance
- An additional complication, like a trap, weather change, theft, moral dilemmas, etc.
This really just boils down to setting a conventional meaning for the dice colors, and creating a few 2d6 tables.
Here's a procedure that I've been using a bit:
-
Roll the Tension Dice pool.
-
If there's at least one skull, an encounter occurs.
-
Count the skulls. These are the three 'levels' of difficulty/impact:
💀: Low / Common, 40% chance
💀💀: Medium / Uncommon, 20% chance
💀💀💀+: High / Rare, 5% chance -
Group the dice by color, add them up, and consult the table.
RED: Creature Type
GREEN: Creature Activity
BLUE: Environment Feature -
For encounter starting distance in feet, take the blue Environment Feature value and multiply it by 10.
-
If additional complications are warranted, find the total value of the red, green and blue dice and consult the 6-36 table.
Here's an example of several tables I used recently when running DDAL-DRW11:

(NOTE: additional complications table not shown above)
Objection, Your Honor! #
But, you may object, you can't just do that, assign different meanings to the same dice roll!
Yes, you can, I just did.
I do realize using values in this way isn't independent, so they're not as random as separate dice rolls, and will be weighted a bit toward one or more of the values being a '1'. I don't really mind, personally, and find that the elegance and efficiency of a single roll makes up for the loss of true randomness.

